FEA mesh using open source tools
The Internet is full of beautiful 3D mesh examples, but it is difficult to get clues about how they were constructed. In fact, creating a good 3D FEA mesh can be very painful without the right tools or training. Furthermore, most of commercial pre-processing software have been improving and propose powerful 3D meshing algorithm, capable of building hybrid or full hexahedron mesh. The aim of this tutorial is to give an overview of the constraints involved when building a 3D mesh for FEA, as well as exposing various meshing methods relying on free and open source tools.
What you need to know about FEA mesh
Before we start, let's give some background information about 3D mesh construction. Usually a 3D mesh can be composed of 4 types of elements:
- tetrahedron (4 corners),
- wedge (6 corners),
- hexahedron (8 corners),
- and rarely pyramids (5 corners).
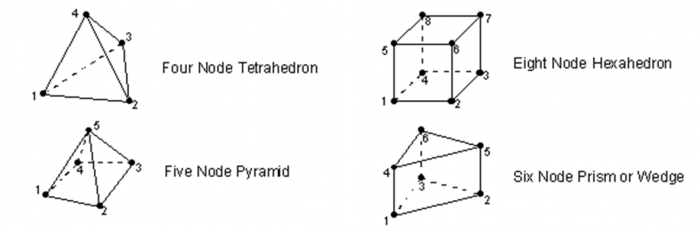
The goal is to get a mesh with the lowest number of degrees of freedom (“dofs”), while maintaining a good representative capability. We may be tempted to race for tetrahedrons, which have only 4 nodes (for a linear element). But reality is more involved: certain types of elements behave better than others. Without entering to much into the details, we can provide some hints about this:
- 4-node tetrahedron (linear element) must be avoided as mush as possible. It behaves poorly and a lot of them are needed to get meaningful results. If you have no other choice, try to convert them to 10-node tetrahedron which is much better.
- if you want to stay with linear elements, you must aim towards hexahedron. Most finite element software (you can guess that SesamX is part of them) propose an improved version of the hexahedron element. That makes it a better choice than the other elements.
- 6-node wedge (linear element) is better than 4-node tetrahedron but worse than 8-node hexahedron. It is ok to use them, but go for hexahedron wherever possible.
- I have not tested the pyramid enough to give relevant advice. Nevertheless, from the fact that this element is seldom used in 3D mesh, this article will not shed light on it.
It is easy to build a full tetrahedron mesh using an automatic mesher (and it is widespread among various software). On the contrary, full hexahedron or hybrid automatic meshers are more involved and harder to find (you can find them among commercial solutions but almost not among free ones).
However, using only free and open source tools, we are still able to build quality 3D meshes.
The remaining of this article exhibits 4 methods to build 3D meshes using Salome or Gmsh. The goal is not to enter into every detail about the options used, but to give an overview of how 3D meshes can be built. Whatever the tool we use, changing the element order is usually a trivial task (either linear or quadratic). Therefore I will not detail it here. Instead, I will focus on controlling the element shapes while meshing.
For each method, I provide a step by step guide with illustrative screenshots. And, when appropriate, I also provide the final result file that you can edit and modify on your own.
Geometry to mesh
I will use the following con rod to showcase how to build each mesh.
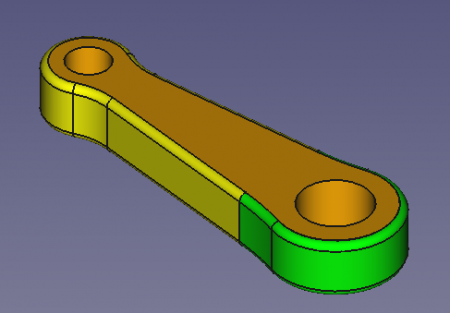
One important feature to mention here, is that this con rod geometry is made of a compound of 3 solids (this reason will make sense when talking about the hybrid mesh generation method) corresponding to each color on the image above.
You can find the corresponding step file here
Full tetrahedron automatic FEA mesh
As mentioned before, it is pretty straightforward to get a full tetrahedron mesh. To build this mesh, we use Salome.
First, we go to the geometry module and import the step file. The Salome tree should look like this:
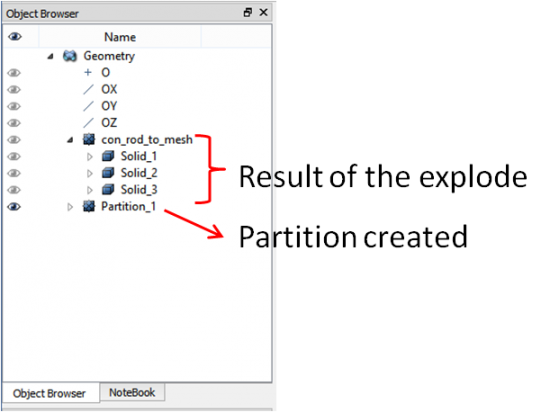
Then we have to explode the compound geometry into its 3 sub-solids and create a partition from these solids. This step is necessary to ensure that Salome will merge coincident nodes from each solid faces. The result tree is then:
Next we go to the mesh module, and create a new mesh on the partition. Under algorithm we can select “NETGEN 1D-2D-3D” and under hypothesis “NETGEN 3D Simple Parameters”. Finally we have to input the edge size that our elements should have.
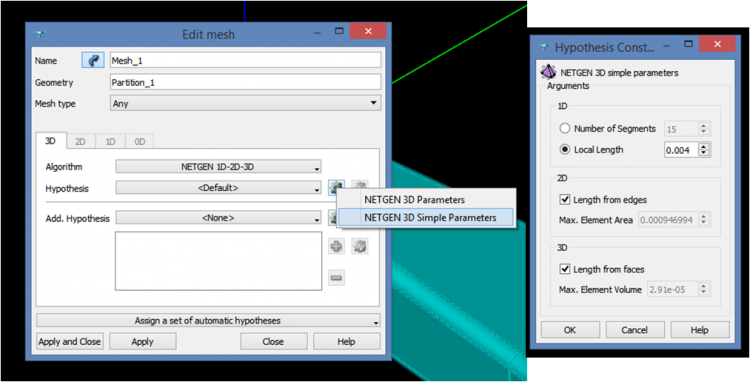
Eventually we have to right click on the mesh and hit “Compute”. The mesh should look like this:
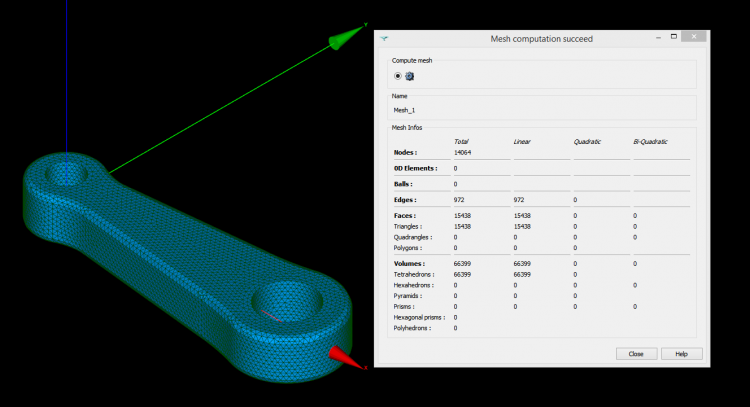
As you can see, the mesh is made of tetrahedron but also triangles and edges elements. To get rid of the 2D and 1D elements, the first step is to click on the mesh and select “Create Group”. A panel appear and we can create one group containing all the 2D elements (as shown on the picture below) and similarly for the 1D elements.
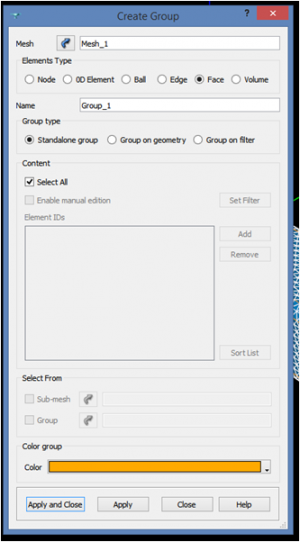
Next to delete these elements, we have to right click on each group and select “Delete Group with Content”. And we get the following full tetrahedron mesh.
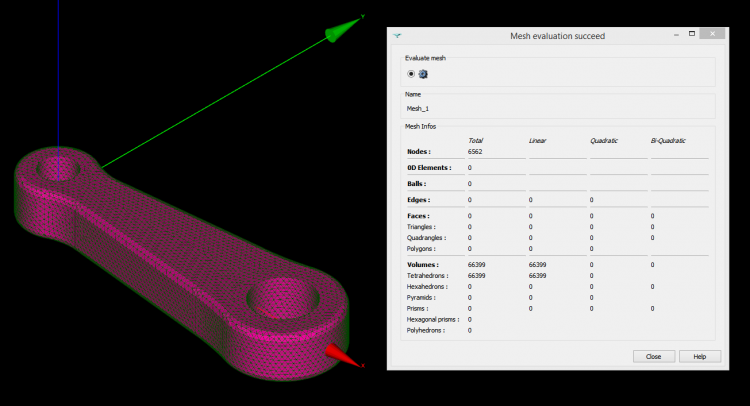
Finally, to check that the mesh does not contain any duplicated nodes we have to select the mesh and use “Controls / Node Controls / Double Nodes”.
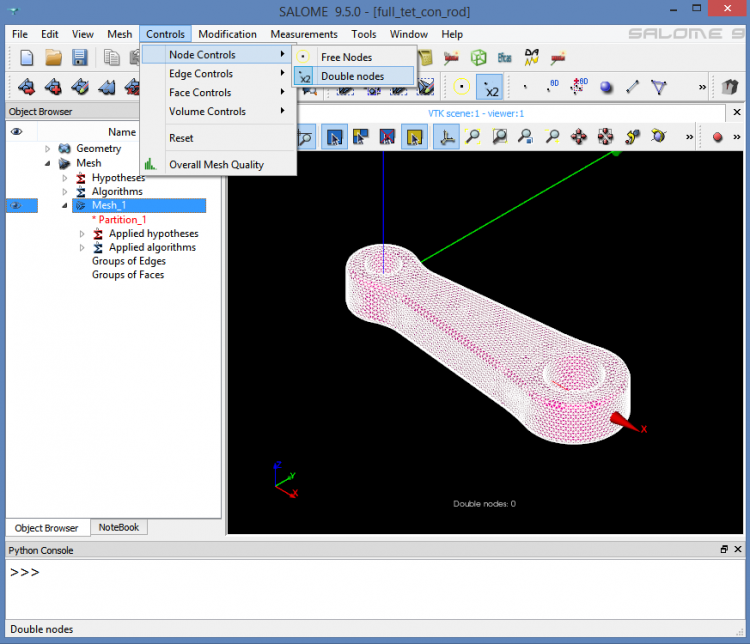
If you want to manipulate this mesh, you can download the corresponding Salome database.
Full hexahedron automatic FEA mesh
Next come the full hexahedron mesh. To build this mesh, we use Gmsh.
First, it is necessary to create a volume physical group containing the 3 solids of the model. It ensures afterwards that the mesh export will, in fact, export only the 3D elements.
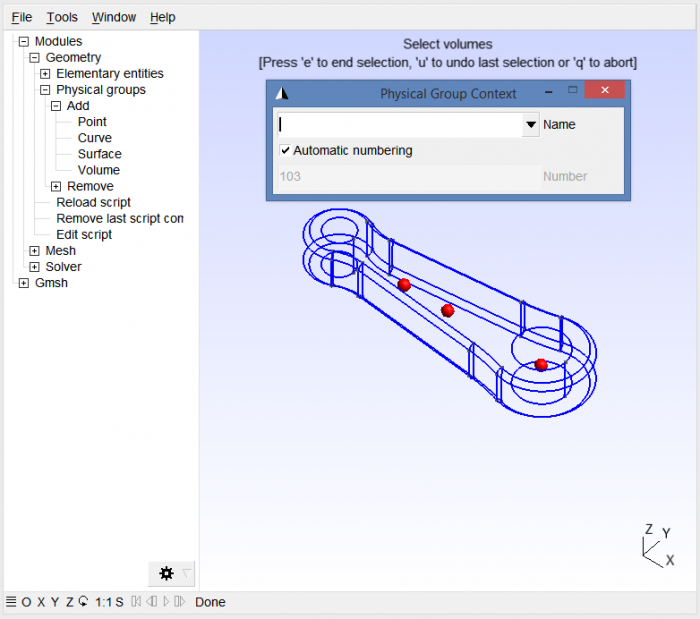
Next we go to “Tools / Options” then “Mesh / General” to select the meshing parameters. We can choose whatever makes it for the 2D algorithm, 3D algorithm and 2D recombination algorithm. These parameters influence how the mesh is built, feel free to change them to notice the difference in the mesh. As a first guess, we can stay with “Delaunay” and “Blossom”. However, make sure to select “All Hexas” as the “Subdivision algorithm” so that the volumes will be filled with hexahedron only.
Finally under “Min/Max element size” we can fix the element size.
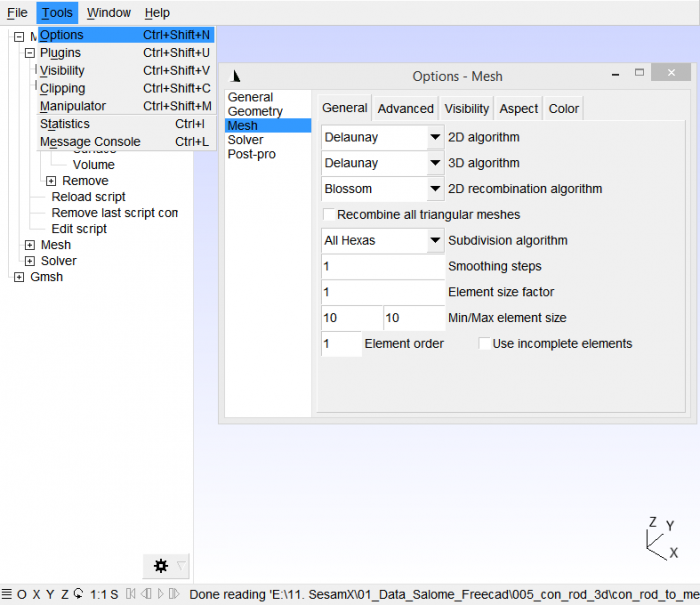
Eventually, we have to go back to the Gmsh tree and click “3D” under “Mesh” to build the mesh.

We can check the mesh content under “Tools / Statistics”. As you can see, the mesh is made of 1D, 2D and 3D-hexahedron elements. Because we have created a physical group for the 3 volumes, only the 3D mesh will be exported.
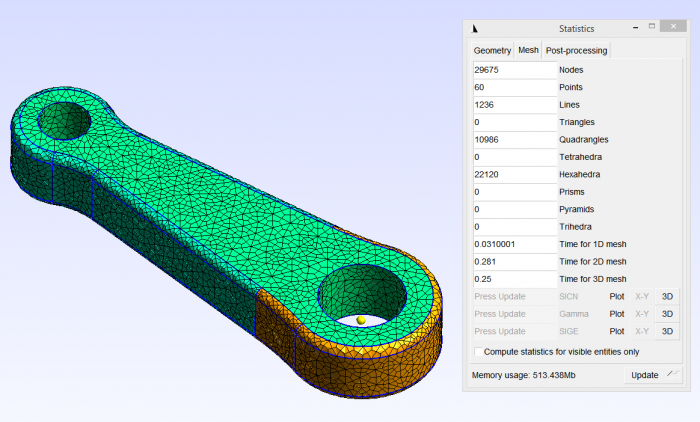
If you have troubles visualizing the 3D elements, you can adjust the visibility parameters in the “Mesh” options window under the “Visibility” tab.
Unfortunately, there is a trap here. The mesh obtained has duplicated nodes at the interfaces between the 3 solids. To visualize them, we can export the mesh as a .med file, import it in Salome, and use the “double nodes” tool mentioned previously.
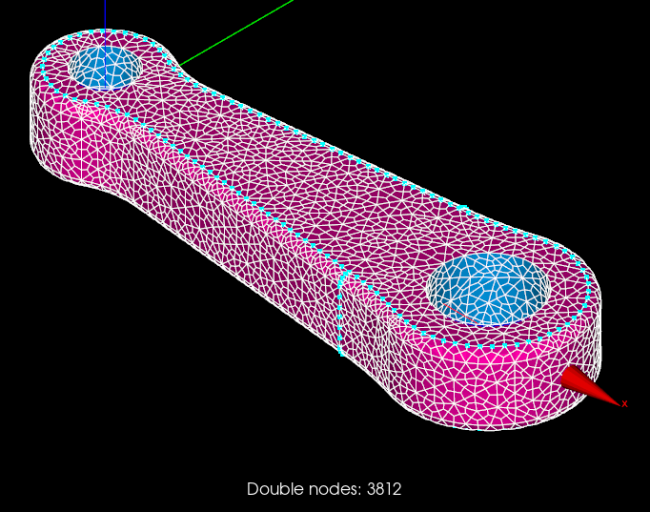
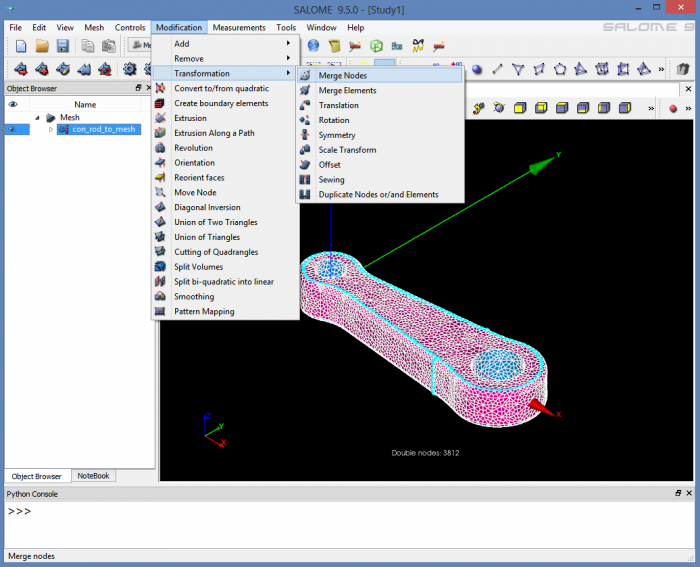
Finally, to solve this issue, we have to use the “Merge Nodes” tool under “Modification / Transformation”.
Hybrid FEA mesh
Next I am showcasing how to build an efficient hybrid mesh with Salome. This method is my favorite because it leads to a well structured mesh, which can capture more efficiently the details of the geometry (if you have a close look to the automatic tetrahedron and hexadreon meshes, you can see that the fillet is not always “well captured” for instance). The drawback of this method is that it does not lead to a full hexahedron mesh but an hybrid mesh made with a majority of hexahedrons, and a minority of wedges used to fill gaps.
The 3D mesh will be built first by meshing 2D surfaces and then by extruding them. To make this process workable, the geometry has been split into 3 solids beforehand. Each of these solids can then be meshed as an extrusion of the surface meshes.
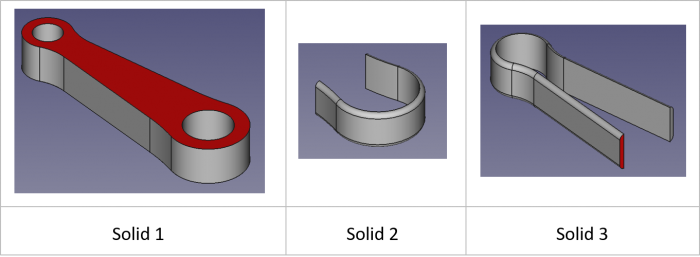
As explained for the full-tetrahedron mesh, we first need to explode the compound geometry and build a partition.
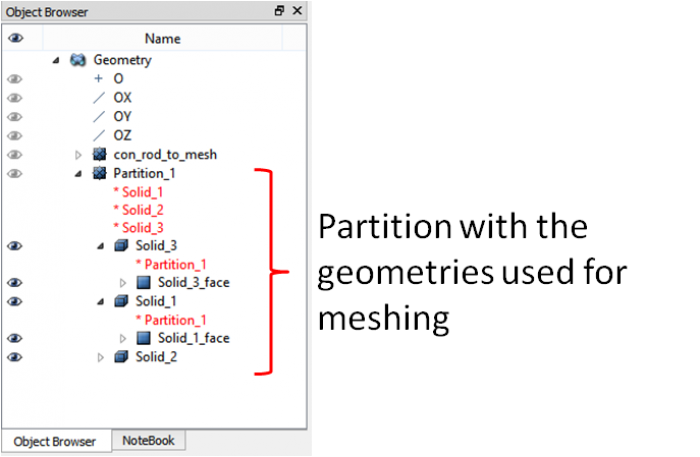
Then, in order to build the 2D meshes on the surfaces and the 3D extrusion meshes, we need to extract (using explode) the relevant geometries from this partition:
- the 3 solids geometries,
- the top face of solid 1 (red face on solid 1 image), that will drive the 3D mesh on solid 1,
- the “fillet face” of solid 2 and 3 (red face on solid 3 image) that will drive the 3D mesh on solid 2 and solid 3.
The Salome tree should look like this:
Next, we go to the mesh module. The meshing process is the following:
- Create a mesh object and assign default 3D mesh parameters to the whole partition,
- Create 2 sub-meshes for the 2 surfaces to mesh,
- Create 3 sub-meshes for the 3 solids to mesh.
The default 3D meshing parameters will not be used while computing the mesh, because the sub-meshes definition will cover the whole partition. Nevertheless, Salome still requires these default parameters.
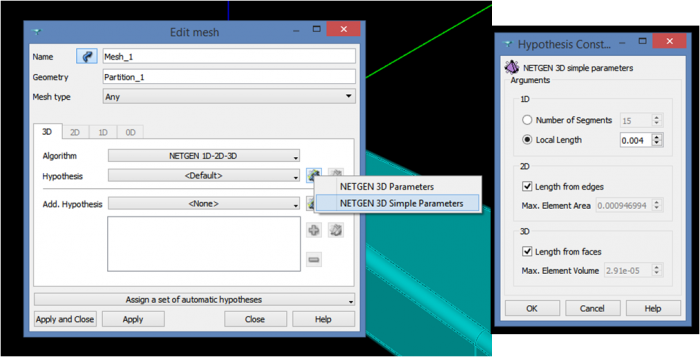
To create the faces sub-meshes, we have to right click on the mesh and select “Create Sub-mesh”. We then need to select one of the faces and choose the “NETGEN 1D-2D” algorithm with “NETGEN 2D Simple Parameters”. Then we can input the element size and make sure to check “Quad-dominated” (to avoid at most triangles).
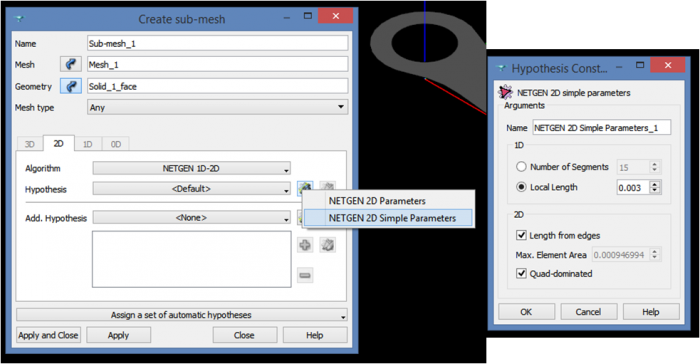
To compute the sub-mesh, we have to right click on it and select “Compute Sub-mesh”. And we repeat these operations for the second face.
Creating the 3D sub-meshes is similar. Once we have selected the solid to mesh, we choose “Extrusion 3D” as the meshing algorithm and no hypothesis needs to be associated. However, we have to provide the 1D algorithm and hypothesis to define how the mesh extrusion should behave.
We select “Wire Discretisation” as the 1D algorithm, and the previous local length used for the 2D sub-meshes as the hypothesis.
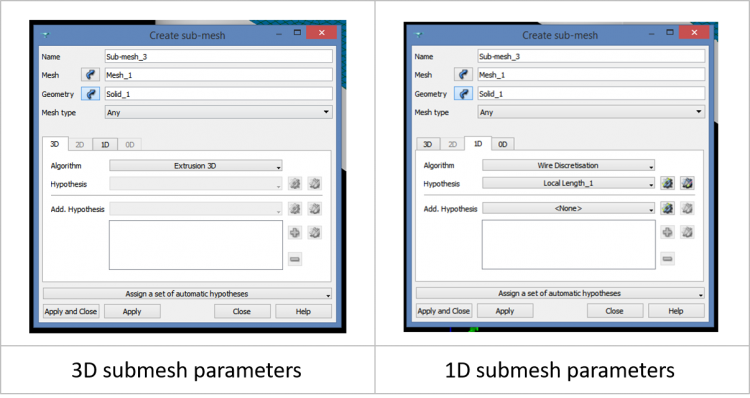
We repeat this for the 2 other solids. The mesh tree should look like this:
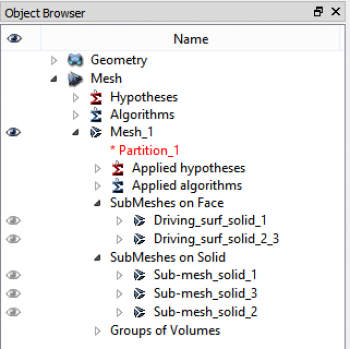
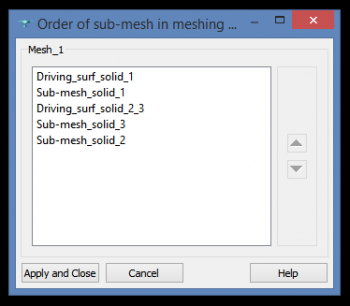
Before computing the mesh, we need to tell Salome in which order the sub-meshes should be computed. To avoid meshing conflict while extruding, it is best in our case, to fully mesh solid 1 before meshing the driving surface of solid 2 and solid 3. We have to right click on the mesh and select “Change sub-mesh Priority”. The meshing order should be the following:
After computation is complete, we can do the same trick as for the full tetrahedron method to remove useless 1D and 2D elements.
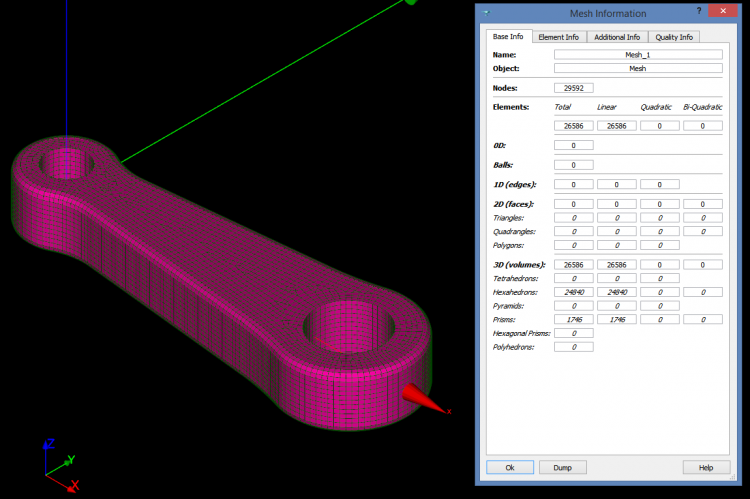
As you can see, this mesh is much more regular than the 2 previous automatic meshes, and the fillet details are better captured.
If you want to manipulate this mesh, you can download the corresponding Salome database.
Hexahedron block FEA mesh
From my point of view, this method is not practical to use on complex shapes. But it is an important one that deserves some explanations. This method allows to build well structured full hexahedron mesh by splitting the volume into blocks.
It is often used for CFD mesh. Applying this method to FEA is a bit harder and requires time and efforts to build the blocks from the CAD geometry.
Some tools offered by Salome allow you to build more efficiently a “block-ready” geometry, but I believe that conceptually they break the whole design workflow. Usually, we start building a CAD model and then we start the meshing process. During this process, we may have to simplify the geometry (removing small holes for instance), to finally mesh it with methods like the ones exposed previously.
On the other hand, when using “block-ready” geometry tools during the meshing process, we are constructing geometries from scratch at the meshing level. Which is not among the duties of the meshing process. And the link between the mesh and the CAD is lost.
Nevertheless, it is still interesting to illustrate what a block mesh is, using Salome. Creating blocks for the con rod model is painful, I prefer to use the tools offered to build directly a cylinder block geometry as an example.
First, we go to geometry and under “New Entity / Blocks” select “Divided Cylinder”. Then we input a radius and an height for the cylinder, and check the “Square Division pattern” (this pattern tells Salome how it should divide the cylinder into blocks).
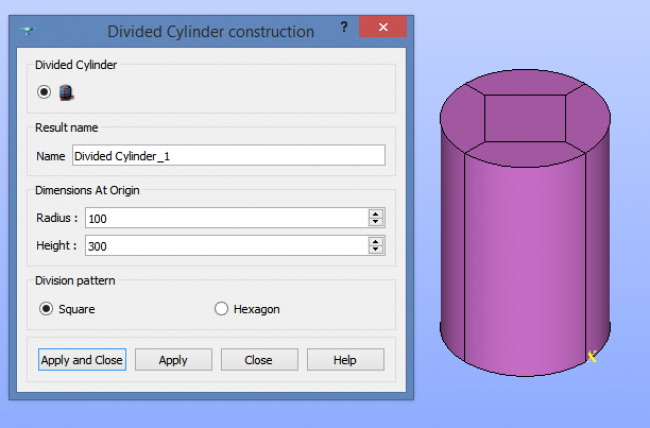
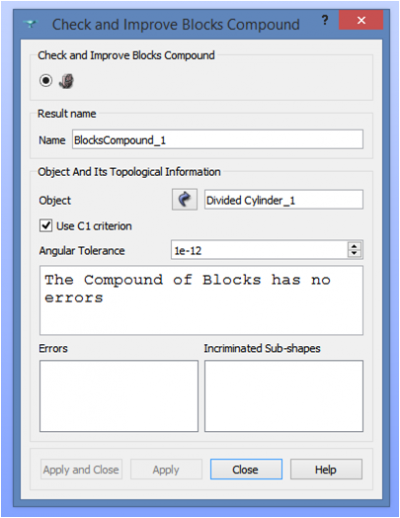
As we can see from the subdivision on the previous image, each block is in fact a solid made of 8 corners, 12 edges and 6 faces. I let you check that our solid as a whole is made of valid blocks using the tool “Check Compounds of Blocks” under the “Inspection” menu.
Next we go to the mesh module and add a new mesh. For the 3D algorithm we select “Hexahedron (i,j,k)”. For the 2D algorithm we select “Quadrangle: Mapping” and choose the “Standard meshing pattern” under Hypothesis. For the 1D algorithm we select “Wire Discretisation” and “Number of Segments” as the hypothesis. We have to input the number of segments instead of a length, because each edge of the block must have the same number of nodes (otherwise Salome will not be able to build the mesh).
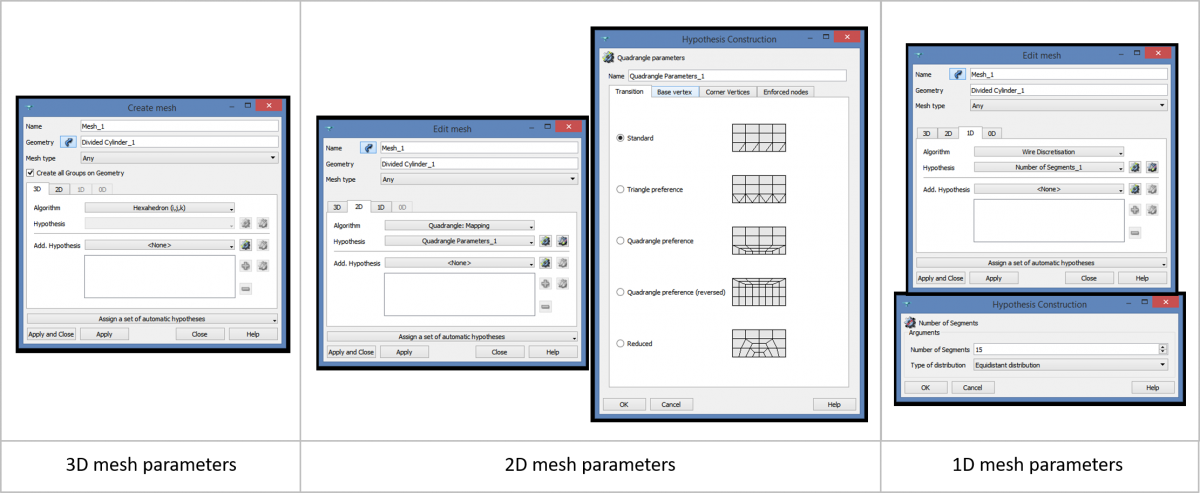
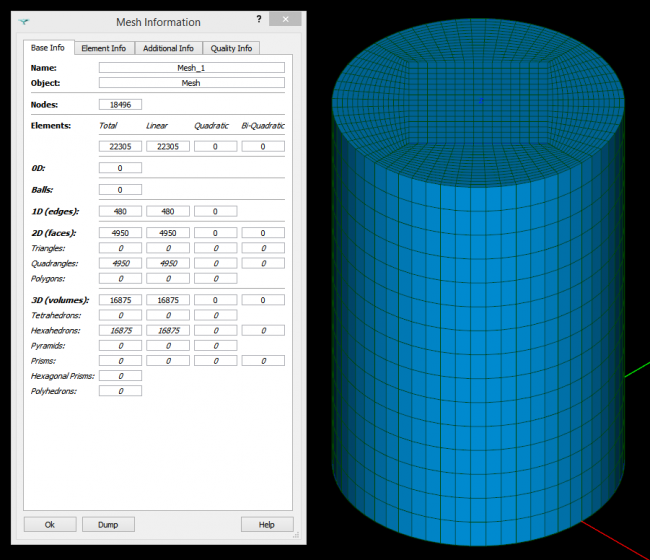
Eventually, we can compute the mesh and check its content. Volumes are made of hexahedron only, and yes, I was lazy and I have not removed the 1D and 2D elements :).
If you want to manipulate this mesh, you can download the corresponding Salome database.
Conclusion
I hope you have gained a better insight about how to build 3D meshes from these examples. Of course, when building a complete assembly you can mix these methods depending on the part you are trying to mesh. From my personal experience, I use the following rules:
- if the part can be described as a compound of extruded solids, I will use the hybrid extrusion method with linear elements.
- if the part has a complex geometry but is not crucial to the whole model, I will use the automatic tetrahedron method with linear elements (and make sure after the computation that in fact, stress gradient are small).
- if the part has a complex geometry and is crucial to the whole model, I will use the automatic hexahedron method with linear elements. If the mesh computation fails (sometimes it can on complex geometries), then I will fall back to the automatic tetrahedron method using quadratic elements.
And of course, do not forget to perform a convergence analysis to validate your mesh.